…and how, ultimately, the Magic Square is related to the Tic-Tac-Toe game
Q1: We have the numbers 1,2,3,…,9 and a 3×3 grid. How do you put the numbers into the grid so that each row, each column, and each diagonal have the same sum (to make a Magic Square)?
Fact 1: There is really only one 3×3 Magic Square with the numbers 1 through 9.
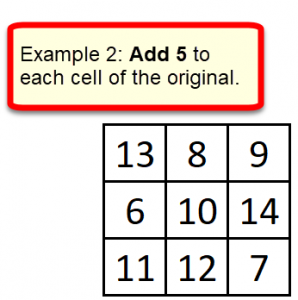
We will consider the Magic Square at the right to be 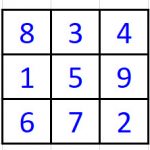 the Magic Square. All other 3×3 Magic Square are equivalent to this, using reflection (horizontal or vertical) or rotation (90°, 180°, or 270°), or a combination.
the Magic Square. All other 3×3 Magic Square are equivalent to this, using reflection (horizontal or vertical) or rotation (90°, 180°, or 270°), or a combination.
When we add each row and each column and each diagonal, we get 15. We will assume the sum must be 15
Let’s see why there is only one Magic Square:
-
-
- Q2: Using the numbers 1-9, make a list of all the ways you can add up 3 numbers to get 15.
-
Fact 2: Using the numbers 1 through 9, three at a time, there are exactly 8 ways to get a sum of 15.
Answer:
1.5.9; 1.6.8; 2.4.9; 2.5.8; 2.6.7; 3.4.8; 3.5.7; 4.5.6.
(By the way, 15 is the only sum for which you can do this — and this is the reason the sum must be 15.)
-
- Notice that some of the numbers get used twice (for example, 1), some 3 times (for example, 6), and one number (5) gets used 4 times!
- The numbers 1,3,7,9 that are used twice, must go on the sides.
- The numbers 2,4,6,8 that are used three times, must go in the corners.
- The number 5 must go in the center, because it is used 4 times in the list above.
.
- Notice that some of the numbers get used twice (for example, 1), some 3 times (for example, 6), and one number (5) gets used 4 times!
- Q3: How do you build the Magic Square logically?
Fact 3: To build THE Magic Square, start with 5 in the middle, put 1 on a side, fill in the 9, put in 2 in a corner, then finish the other cells, making each sum 15.
Here is the process:
 Q4: How do you make other 3×3 Magic Squares, using different numbers.
Q4: How do you make other 3×3 Magic Squares, using different numbers.
Fact 4: To build additional Magic Squares use the original Magic Square and multiply each cell by a number or add a number or both.
- Here are three examples:
 Q5: If each cell of a Magic Square is multiplied by M and then B is added, to make a new Magic Square, what is the new magic sum (sum of each row, column, and diagonal)?
Q5: If each cell of a Magic Square is multiplied by M and then B is added, to make a new Magic Square, what is the new magic sum (sum of each row, column, and diagonal)?
Fact 5: If the original magic sum of a Magic Square is S, then the new magic sum (when you multiply each cell by M and then add B) is M×S + 3×B.
If you don’t mind a little algebra, here’s why: You might check this by finding the magic sum in the three examples above.
You might check this by finding the magic sum in the three examples above.
Q6: How is the Magic Square related to the Number Scrabble Game?
Number Scrabble (also known as Pick 15) is a number game where players take  turns selecting numbers from 1 to 9 without repeating any numbers previously used. The first player to get three* of their own numbers to total exactly 15 wins the game. (Sometimes number tiles are used to play the game.)
turns selecting numbers from 1 to 9 without repeating any numbers previously used. The first player to get three* of their own numbers to total exactly 15 wins the game. (Sometimes number tiles are used to play the game.)
(*I believe the game can also be played allowing for any number of numbers to total to 15 [for example 4 numbers], but under these rules, a knowing player would never allow their opponent to win with 4 numbers.)
Fact 6: If the numbers (1-9) are placed in a 3×3 Magic Square, then the Number Scrabble game is equivalent to the game of Tic-Tac-Toe!
This means that, the way you win (or the game ends in a draw) in Tic-Tac-Toe is the same as the way you win (or the game ends in a draw) in the Number Scrabble game (and vice versa).
The reason for this is Fact 2. There are exactly 8 ways to combine 3 numbers to get a sum of 15. All 8 ways are represented in the Magic Square.
For example, in Tic-Tac-Toe, one player uses an o, which means that’s my spot (or my 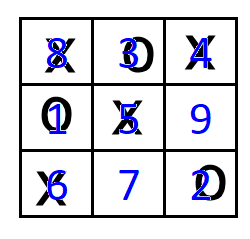 number in Number Scrabble). The other player uses an x to mark their spot.
number in Number Scrabble). The other player uses an x to mark their spot.
In the example shown, X wins by getting 4, 5, & 6 (which total 15) which is three in a row on the Tic-Tac-Toe board.
Closing remark: It is useful to understand how the game of Tic-Tac-Toe works. (There is a short list of possibilities.) There is no winning strategy. There is a good strategy and there is a way to force a draw. We’ll leave the details for another day. The aha moment for me was at a Junior High Youth Group meeting at our church (Iowa City, IA). We had 9 chairs put out, in 3 rows of 3. We went (in two teams) out an sat in the chairs (one by one). Standing on the sideline I began to see how it worked.