This page is designed to provide links and information for understanding Euclidean Geometry in its original form.
Euclid’s Elements site from Clark University* – Introduction, TOC, Book 1, Quick Trip. This is a good, comprehensive treatment of http://aleph0.clarku.edu/~djoyce/java/elements/bookI/cn.html Nice things include ⦿there is Guide (explanation) of the definitions, propositions, etc., ⦿proof of the propositions, ⦿the justification is given for proofs on the right hand side, ⦿how a proposition is used is stated. (*The site appears old, but I believe it still to be very valuable and useful.)
Appendix 1 in Howard Eves A Survey of Geometry, revised edition. Lists the 23 definitions, 5 Axioms, 5 Postulates, and the 48 propositions of Book 1.
Euclid’s First Principles and the Statement of the Propositions of Book 1.
Euclid’s 5th (“parallel”) Postulate
After 1000’s of years of study, mathematicians determined that Euclid’s 5th postulate was, in fact, required (not provable from the first four). There are many statements (propositions in Euclid’s elements) that are equivalent to Euclid’s 5th postulate. Here is a list.
Absolute Geometry
There is a geometry in which neither the Fifth Postulate nor any of its alternatives is taken as an axiom. This geometry is called Absolute Geometry (sometimes called “neutral geometry”). See this article (which I’ll call the Texas article), which includes a proof that Euclid’s five Postulates and common notions imply Playfair’s Axiom (below). Wikipedia, of course, has an article.
Playfair’s Axiom. Through a given point, not on a given line, exactly one line can be
drawn parallel to the given line. Playfair’s Axiom is equivalent to the Fifth Postulate in the sense that it can be deduced from Euclid’s five postulates and common notions, while, conversely, the Fifth Postulate can deduced from Playfair’s Axiom together with the common notions and first four postulates. Included in the article is the Theorem. Euclid’s five Postulates and common notions imply Playfair’s Axiom.
Another article is here, includes a proof that Playfair’s Axiom implies Euclid’s fifth postulate.
Non-Euclidean Geometries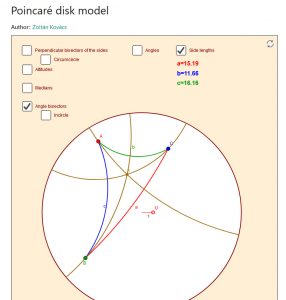
This article is a good starter explanation of non-Euclidean geometry. It has a nice summary chart.
Experiment with the Poincaré disk model of 2-dimensional hyperbolic geometry with this wonderful GeoGebra file.
Experiment with Poincaré’s Half-Plane model (“basic workspace”).
Abraham Lincoln and The Elements
From Lincoln’s biography:
My Presentation
Byrne’s Euclid
In 1847, Oliver Byrne wrote an edition of Euclid’s Elements, the first six books. It stresses color and visualization. MAA description. Can be viewed online here. Internet archive here.


