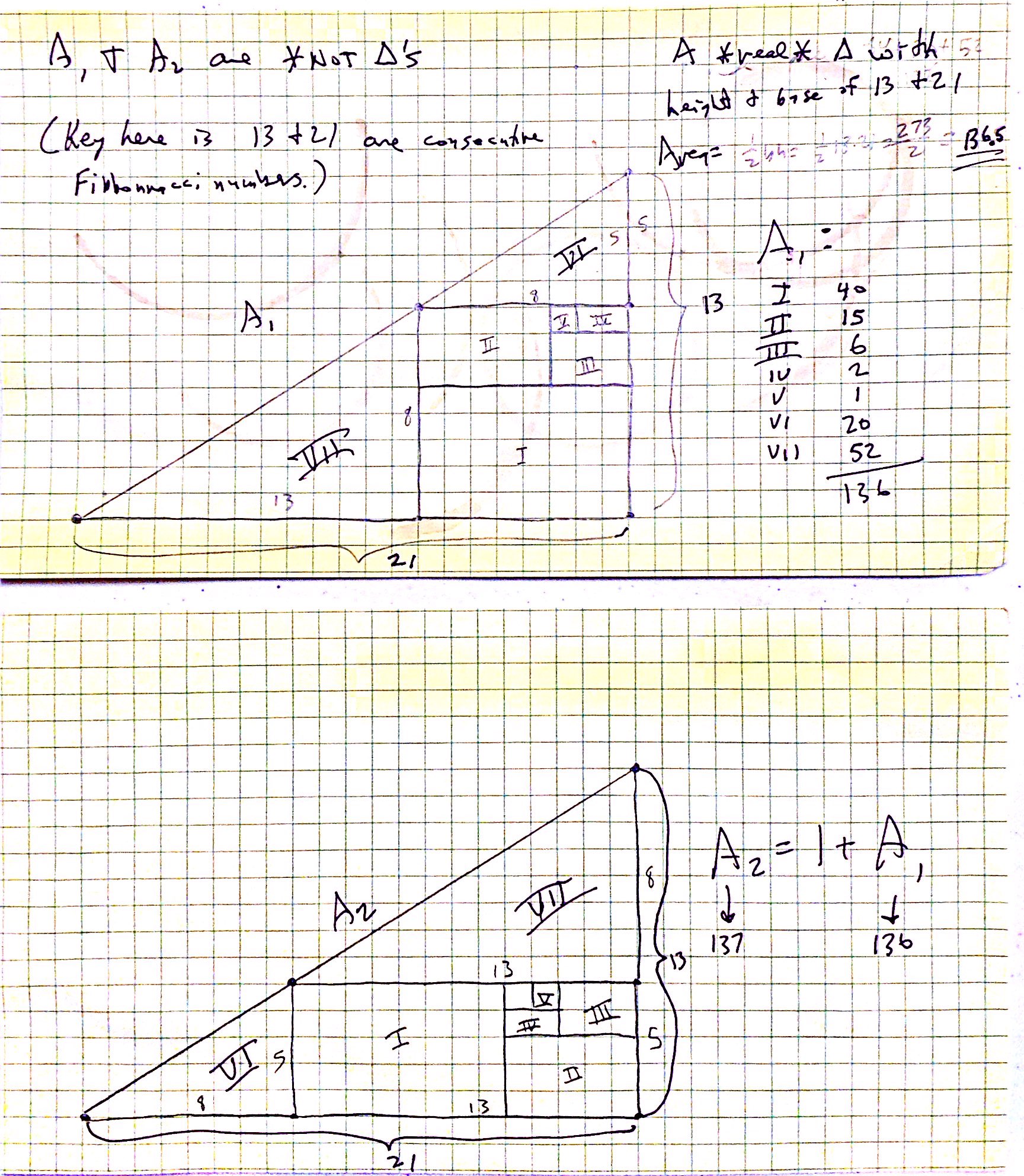
Disclaimer: I apologize for the low quality of this page and diagram. I believe it to be mathematically correct. Someday someone can make it look nicer.
This diagram (OK a better, neater one could be made) shows two would-be triangles. One with an area (if you add up the parts) of 136. The other with an area of 137. Spoiler alert: They aren’t triangles. An actual triangle would have area 136.5. The hypotenuse of the would-be triangles are slightly bent. Since the slope are very close to the same – in face very close to the golden ratio, it looks straight. The reason the slopes are close to the golden ratio is because 13 and 21 are consecutive Fibonacci numbers.